How to run an EcoNet model?
After the model is entered, all the user has to do is to choose a simulation method, adjust the parameters if necessary, and hit "Run Model" to retrieve the results. Note that all the information EcoNet needs to run a simulation already exists in the model, so one may wonder why EcoNet even needs a simulation method and parameters?
| Method type | Method name | Parameters |
|---|---|---|
| Adaptive time-step | Runge-Kutta-Fehlberg | Maximum-time, Sensitivity |
| Fixed time-step | 4th-order Runge-Kutta | Total-time, Step-size |
| Stochastic, Fixed time-step | Langevin Equation | Total-time, Step-size |
| Stochastic, Adaptive time-step | Gillespie's method | Total-time |
Like any other simulation software, EcoNet converts the entered model into a differential equation system, the solution of which is the time-course data of storage values of all compartments. Unfortunately there is no magic numerical method capable of solving any given differential equation without human intervention. Depending on the complexity of the model, the user may need to choose a different numerical method or adjust parameters. EcoNet makes this an easy and simple task.
In most cases, the default method and parameters will work, and no adjustment will be necessary. The default method (Runge-Kutta Fehlberg) is an adaptive algorithm, meaning that it continuously adjusts itself to the complexity of the solution on the fly. Any problems with the solution can be remedied simply by adjusting the Sensitivity parameter. This parameter is correlated to the amount of error allowed between the actual solution and the numerical solution. The smaller the Sensitivity parameter, the higher the accuracy. However accuracy does not come free, as EcoNet will take longer to run when smaller Sensitivity values are used. Keep in mind that this relation is not linear, so decreasing Sensitivity by half might take EcoNet ten times longer to run. If EcoNet takes too long to run, or terminates early, the first thing you should try is to increase the Sensitivity value.
The other parameter is Total time, which is basically the simulation length of the model in time units. In other words, it is the largest value on the x-axis of the time-course plot of all storage values (See Figure below). A particular time unit is not specified, because it has to be consistent with the user-defined flow coefficient units. So we leave it up to the user to choose the appropriate set of units for their model. The higher the value of this parameter, the longer the computing time.

|
Troubleshooting
So, what if something goes wrong and one needs to adjust the simulation parameters to fix the situation, what would be the best strategy? Here are the most common issues:
- EcoNet takes too long to run, or terminates early. If you are using the deafult Adaptive time-step method, increasing the Sensitivity value will most likely solve the problem. If this does not work, we suggest that you switch to Fixed time-step method, and experiment with various step-size values. EcoNet will always return accurate results in a couple of seconds for small enough Step-size and Total-time parameters, no matter how complicated the model is.
- EcoNet runs but the results look unrealistic. This means that the numerical solution is not accurate. The solution is to decrease the Sensitivity or Step-size parameter. This action will increase accuracy, but Econet will take longer to finish the simulation. If it takes too long, then try decreasing the Total time parameter, or switch to Fixed time-step method, and experiment with smaller step-size values.
Note that there is a trade-off between accuracy, computing time and Total time. Rest assured that the numerical engine of EcoNet is much faster than that of commercially available software such as Matlab and Stella. Therefore finding a good balance between accuracy and speed should not be a difficult task.
Numerical Solution Methods
Understanding the meaning of step size requires some numerical analysis knowledge. Although such knowledge is not necessary to run EcoNet, we would like to provide some additional information for the interested user. We already mentioned that EcoNet converts the model into a differential equation system.
This differential equation can be fairly complex, which makes it extremely hard to find the exact analytic solution. Therefore, all simulation software uses numerical solution methods, which are iterative computer algorithms that construct approximate solutions. A successful numerical solution will have negligibly small error relative to the analytic solution. Fixed time-step methods construct the solution step-by-step in time, assuming that the solution does not change rapidly during each time step.

|
This assumption is the main reason for error; rapid changes in the solution may be missed if large step-sizes (dt) are used. Therefore small step sizes are desirable for accuracy, but using extremely small values will increase the computation time if Total time remains the same:

Adaptive numerical methods, such as Runge-Kutta-Fehlberg, have an error detection mechanism that continuously monitors the solution accuracy at each iteration. If it detects that the error is larger than the Sensitivity parameter defined by the user, it automatically decreases the step-size and repeats the iteration. Similarly, if it senses that the accuracy is much smaller than the Sensitivity parameter, it increases the step-size. This way, an adaptive scheme continuously optimizes speed for a given accuracy.
Although this sounds like the perfect numerical method, the weak link in adaptive methods is the error detection mechanism. One can never find the exact error without knowing the exact solution. When the ``detected'' error and the actual error are not the same, the solution may not be accurate, or the simulation may take longer. However this rarely happens, and adaptive schemes are preferred over fixed step-sized methods in general. We refer the interested users to numerical analysis texts for more information [13].
Stochastic Method
The third simulation method offered by EcoNet is a stochastic algorithm. Stochastic solvers take the probabilistic system behavior into account and generate different solutions at each run. It seems that stochastic solvers are producing random results. To the contrary, in most cases stochastic solutions are more accurate because no real biological or ecological system is deterministic in nature. It only makes sense to use a stochastic solver for a system which is stochastic in nature.
EcoNet features a fast stochastic method based on the Langevin equation [10]. It is as easy to use as the previous two methods. The parameters, Total time and Step size, are exactly the same as in the 4th-order Runge-Kutta method, and so is the strategy to adjust the parameters for accurate results.
Users should not confuse a stochastic solution with a deterministic solution driven by a noisy input, or a deterministic solution perturbed randomly at each iteration step. Although these practices will generate random behaving solutions, the noise-term associated with these solutions is wrong, which negates the very advantage of using a stochastic solution method in the first place. This is not a trivial fact, and we refer the interested user to further reading [6,10]. In simple terms, a stochastic process representing a stock-flow model should be compatible with the so called master equation [9]
This is not an easy condition to satisfy, and true stochastic solvers are complex and hard to implement. This is the main reason why very few software programs feature stochastic methods. Since they are not widely available, few users are aware of their power. For example, a single stochastic solution will reveal the inherent variations in the stock values, eliminating the need for many repeated runs for sensitivity analysis.
|
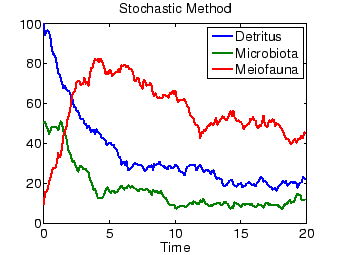
The figure above shows the time-course data of a simple EcoNet model produced using the 4th-order Runge-Kutta method and the stochastic method. It seems that stochastic solutions always look like the noisy versions of their deterministic versions. This is not true in general; there are cases where only a stochastic method will provide an accurate representation of the modeled system. For example, if the flowing matter in the system exists in scarce discrete quantities, or if the system is capable of multiple steady states, deterministic and stochastic methods may differ significantly.
From Model to Differential Equation
EcoNet automatically converts the entered model into a differential equation system, and solves it using the chosen method and parameters. This equation system is never displayed explicitly, and there is no need to do so. Still, here we explain how EcoNet does this conversion for the interested user. Let's consider the following simple model:
* -> Detritus c=10 # input to Detritus Detritus -> Microbiota c=0.15 # flows Detritus -> Meiofauna c=0.2 # among Microbiota -> Meiofauna c=0.5 # compartments Meiofauna -> * c=.23 # outputs Microbiota -> * c=.01 Detritus = 100 # initial storage values Microbiota = 50 Meiofauna = 10 |
Let's focus on the compartment Microbiota. The storage value of Microbiota is controlled by the three underlined flows. The first flow is an input to Microbiota, while the last two are outputs from Microbiota. Therefore we can express the storage value change of the Microbiota compartment as follows:
![$\displaystyle \frac{d\,[\texttt{Microbiota}]}{dt}$](img34.gif) | |||
The algebraic expression of flow speeds is determined by the flow type, and the repeated use of ``c='' represents that the only flow type used in this model is donor controlled flow (Mass action). Then based on our previous discussion of flow types, the complete differential equation system is going to be:
![$\displaystyle \frac{d\,[\texttt{Detritus}]}{dt}$](img40.gif) | |||
![$\displaystyle
\frac{d\,[\texttt{Microbiota}]}{dt}$](img34.gif) | |||
![$\displaystyle
\frac{d\,[\texttt{Meiofauna}]}{dt}$](img43.gif) |
The environment is not associated with a limited storage value, so the input from the environment to Detritus is simply represented with the constant 10 in the first line of the equation above. Just as an example, if the third line of the model were replaced with

meaning that the flow is not donor controlled but both donor and recipient controlled (Lotka-Volterra), EcoNet would construct the following differential equation system:
![$\displaystyle \frac{d\,[\texttt{Detritus}]}{dt}$](img40.gif) |
|||
![$\displaystyle \frac{d\,[\texttt{Microbiota}]}{dt}$](img34.gif) |
|||
![$\displaystyle \frac{d\,[\texttt{Meiofauna}]}{dt}$](img43.gif) |
Next: Simulation & analysis results
DHTML Menu By Milonic JavaScript